| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 1차원 DP
- 2차원 dp
- 99클럽
- @BeforeAll
- @BeforeEach
- @Builder
- @Entity
- @GeneratedValue
- @GenericGenerator
- @NoargsConstructor
- @Query
- @Table
- @Transactional
- Actions
- Amazon EFS
- amazon fsx
- Android Studio
- ANSI SQL
- api gateway 설계
- api gateway 필터
- ApplicationEvent
- argocd
- assertThat
- async/await
- AVG
- AWS
- aws autoscaling
- aws eks
- aws iam role
- AWS KMS
- Today
- Total
기록
프로그래머스_python_최적의 행렬 곱셈 본문
문제
https://programmers.co.kr/learn/courses/30/lessons/12942#
코딩테스트 연습 - 최적의 행렬 곱셈
크기가 a by b인 행렬과 크기가 b by c 인 행렬이 있을 때, 두 행렬을 곱하기 위해서는 총 a x b x c 번 곱셈해야합니다. 예를 들어서 크기가 5 by 3인 행렬과 크기가 3 by 2인 행렬을 곱할때는 총 5 x 3 x 2 =
programmers.co.kr
풀이
문제 접근하기
행렬곱셈에는 결합법칙이 성립하므로 행렬을 곱하는 순서에 따라 곱셈의 횟수가 달라진다.
dp를 사용해서 이 문제를 해결할 수 있다.
우선, N*N의 테이블을 작성한다. 테이블의 각 셀에는 아래에 해당하는 값을 적어 넣는다.
dp[시작][끝] = (시작~끝) 범위에 있는 행렬을 모두 곱할 때 최소 연산 수
sizes에 아래와 같은 행렬이 담겨 있다면,

dp[3][8] 는 DEFGHI를 만들기 위한 최소 연산 수이고,
DEFGHI를 만들 수 있는 경우의 수를 생각해보면, 아래와 같다.
| start | middle | end | |
| D + EFGHI | 3 | 3 | 8 |
| DE + FGHI | 3 | 4 | 8 |
| DEF + GHI | 3 | 5 | 8 |
| DEFG + HI |
3 | 6 | 8 |
| DEFGH + I | 3 | 7 | 8 |
그 중 DE + FGHI의 경우를 살펴보면, 필요한 연산의 수는
(DE 연산 수) + (FGHI 연산 수) + 4*3*3 = dp[3][4] + dp[5][8] + S[0]*M[1]*E[1]이다.

점화식 만들기
위의 식을 참고하여 점화식을 만들 수 있다.
(S~E까지 연산수) = (S~M까지 연산수) + (M+1~E까지의 연산수) + 두 행렬을 곱하기 위한 연산 수
dp[s][e] = min(dp[s][m]+dp[m+1][e] + sizes[s][0] + sizes[m][1] + sizes[e][1]), (s<=m<e)
TOP-DOWN
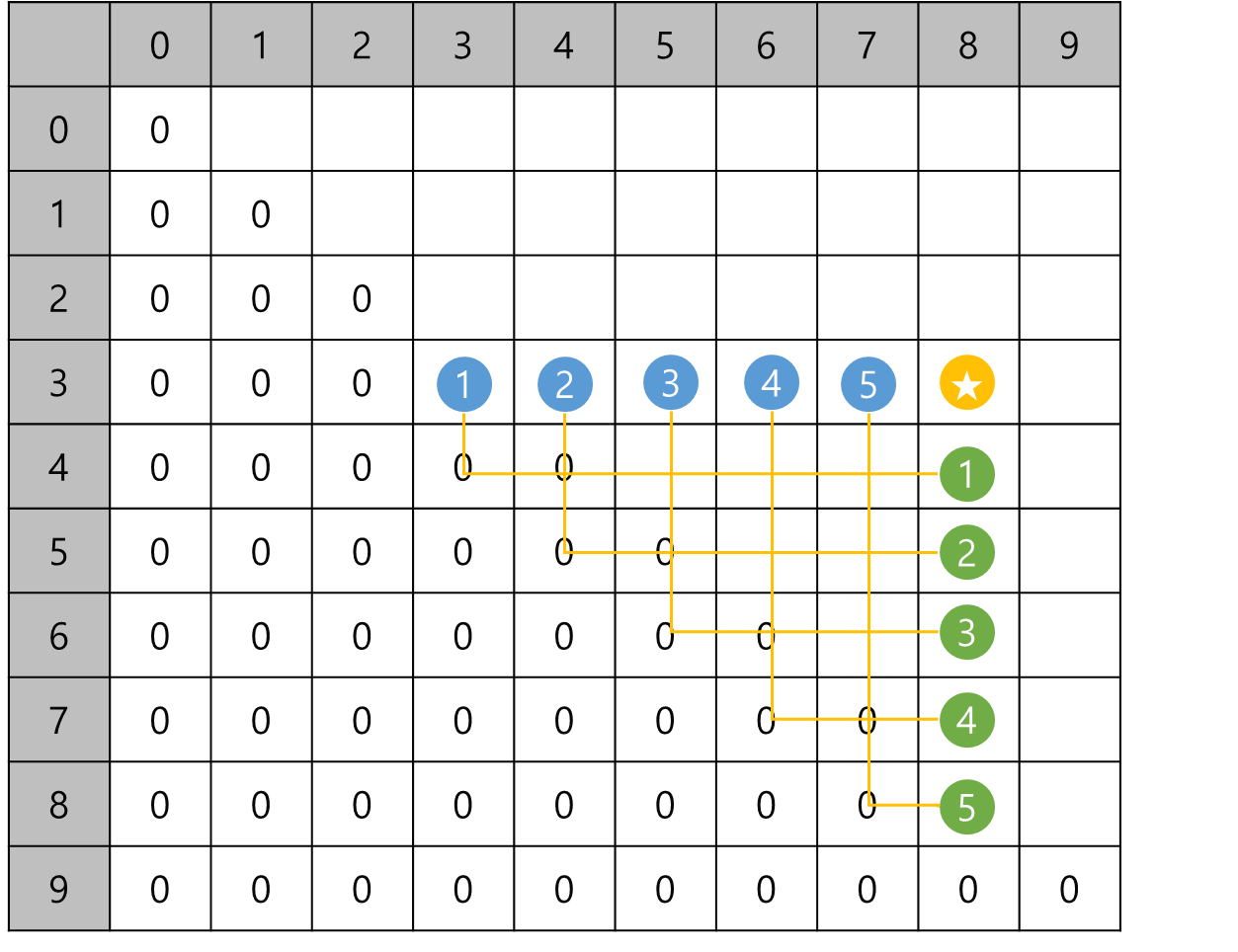
dp[3][8] = min(
dp[3][3] + dp[4][8] + sizes[3][0] + sizes[3][1] + sizes[8][1],
dp[3][4] + dp[5][8] + sizes[3][0] + sizes[4][1] + sizes[8][1],
dp[3][5] + dp[6][8] + sizes[3][0] + sizes[5][1] + sizes[8][1],
dp[3][6] + dp[7][8] + sizes[3][0] + sizes[6][1] + sizes[8][1],
dp[3][7] + dp[8][8] + sizes[3][0] + sizes[7][1] + sizes[8][1]
)점화식에 따라 dp[3][8]을 위처럼 표현할 수 있다. 따라서, 대각선을 따라 dp를 채워나간다.

비슷한 문제
https://www.acmicpc.net/problem/11049
11049번: 행렬 곱셈 순서
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같
www.acmicpc.net
코드
def solution(sizes):
dp = [[0 for j in range(len(sizes))] for i in range(len(sizes))]
for gap in range(1, len(sizes)) :
for s in range(0, len(sizes)-gap) :
e = s+gap
candidate = list()
for m in range(s, e) :
candidate.append(
dp[s][m]+dp[m+1][e]+
sizes[s][0]*sizes[m][1]*sizes[e][1])
dp[s][e] = min(candidate)
return dp[0][-1]
'코딩테스트 > python' 카테고리의 다른 글
| 프로그래머스_아이템 줍기 (0) | 2022.01.08 |
|---|---|
| 프로그래머스_python_올바른 괄호의 갯수 (0) | 2022.01.06 |
| 프로그래머스_python_섬 연결하기 (0) | 2021.12.29 |
| 프로그래머스_python_배달 (0) | 2021.12.27 |
| 프로그래머스_python_모두 0으로 만들기 (0) | 2021.12.26 |



